«Statistiken sind wie Bikinis. Was sie zeigen, ist anregend, aber was sie verbergen, ist die Hauptsache» – Aaron Levenstein.
Angesichts der enormen Datenmengen ist Statistik heutzutage nicht mehr wegzudenken. Dabei werde statistische Berechnungen in praktisch allen erdenklichen Bereichen eingesetzt. Einerseits zur Berechnung von wichtigen Kennzahlen in den verschiedenen volkswirtschaftlichen Themen wie etwa dem Bruttoinlandprodukt (BIP) oder der Inflation. Andererseits spielt Statistik aber auch in der Privatwirtschaft eine ebenso bedeutende Rolle. Von Branche zu Branche gibt es unterschiedliche Anwendungsmöglichkeiten, wo sie zum Zug kommen könnte. Beispielsweise kann im Detailhandel sowie im Online Handel der durchschnittliche Wert des Warenkorbes der Kunden gemessen werden. Anhand dieser Kennzahl kann dann gemessen werden, ob Aktionen oder eine andere Platzierung der Artikel den Warenkorbwert positiv beeinflussen und somit zu mehr Umsatz führen.
In Call-Centern kann die durchschnittliche Bearbeitungsdauer für ein Telefongespräch berechnet werden. Wenn ein gewisser Mitarbeiter deutlich länger für ein Telefonat braucht als der Durchschnitt, kann dies ein Indikator dafür sein, dass der Mitarbeiter zusätzliches Training benötigt. Ein abteilungsweites Training kann sogar bewirken, dass die durchschnittliche Bearbeitungsdauer sinkt.
Statistik kann auch relevant sein, für die Beschreibung des eigenen Angebots. Das Service-Level beziehungsweise der Servicegrad ist eine weit verbreitete Kennzahl für das angebotene Serviceniveau. Im Falle von OCR Software wird das Angebot oftmals mit Extraktionsraten und Sensitivität beschrieben, welche ebenfalls mittels statistischer Berechnungen ermittelt werden.
Wie aber das Zitat von Aaron Levenstein verdeutlicht, können Statistiken zwar schön aussehen und gewisse Indizien liefern, aber die Hintergründe und Berechnungen sind das wichtigste einer jeden Statistik. Graphische Darstellung sowie gewisse Kennzahlen wie etwa Lage- oder Streuparameter sollten nicht isoliert betrachtet werden. Denn wie Francis Anscombe 1973 festgestellt hat, können verschiedene Datensätze zwar die gleiche Varianz sowie den gleichen Mittelwert aufweisen, graphisch aber komplett unterschiedlich aussehen. Doch bevor wir weiter darauf eingehen, beschreibe ich erst kurz die wichtigsten Begriffe.
Was sind Mittelwert, Standardabweichung und Varianz?
Der Mittelwert eines Datensatzes ist ganz einfach der Durchschnitt dieser Daten. Beispielsweise hat der Mittelwert den Wert 10 bei einem Datensatz mit den Zahlen 5, 10 und 15.
Die Standardabweichung ist ein Mass für die Streuung der Werte um den Mittelwert. Bei einem Datensatz mit einer grossen Anzahl an Werten, zeigt die Standardabweichung, wie weit sich diese Daten zwischen dem Minimum und dem Maximum verteilen und wie dicht sie sich um den Mittelwert häufen. Diese Verteilung der Datenpunkte kann in einer Funktionskurve dargestellt werden. Je nach Beschaffenheit der Daten hat diese eine unterschiedliche Form. Haben wir eine Normalverteilung, so ähnelt diese einer Glocken-Form. Beispielsweise bei der Körpergrösse von Fussballern könnte der Mittelwert 1.80m und die Standardabweichung (σ) 0.1m sein. Eher wenige Fussballer sind über 2.00m oder unter 1.60m, aber mehr zwischen 1.70m und 1.90m. Der Grossteil der Fussballer wird innerhalb einer Standardabweichung unter oder über dem Mittelwert von 1.80m liegen. Geht man von einer Normalverteilung aus so wären ~ 68% der Fussballer zwischen 1.70m und 1.90m gross. ~ 95% aller Fussballer würden innerhalb von zwei Standardabweichungen liegen. In diesem Fall wären ~ 95% zwischen 1.60m und 2.00m gross. Die übrigen ~ 5% der Fussballer wären über 2.00m gross oder unter 1.60m gross.
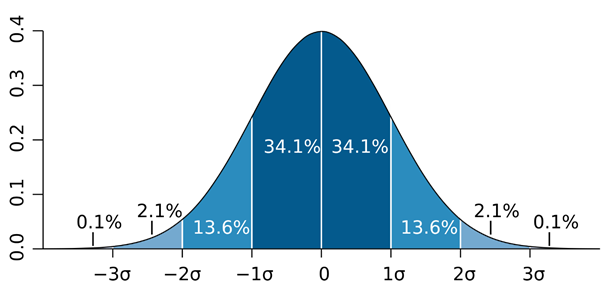
Während die Standardabweichung also zeigt, wie sich die Werte um den Mittelwert verteilen, ist die Varianz lediglich das Quadrat der Standardabweichung und ist somit ebenfalls ein Streuungsmass, das die Verteilung von beobachteten Werten um den Erwartungswert beschreibt. Durch die Quadrierung wird aber auch die Einheit quadriert und so wäre in unserem Beispiel die Einheit nicht mehr Meter (m) sondern Quadratmeter (m2), was in Bezug auf Körpergrösse ein wenig sinnvolles Mass ist.
Zusammenfassende Statistiken erzählen nicht die ganze Geschichte
Diese drei beschriebenen Parameter ermöglichen es, einen grossen, komplexen Datensatz mit nur wenigen Kennzahlen relativ gut zu beschreiben. Aber es besteht die Gefahr, sich nur auf diese zusammenfassenden Statistiken zu verlassen und die Gesamtverteilung zu ignorieren. Die Berechnung von diesen Parametern ist daher nützlich, sollte aber nur ein Teil der eigentlichen Datenanalyse ausmachen. Im Folgenden erkläre ich Ihnen, wieso dem so ist.
Wie vorhin angedeutet, demonstriert das Anscombe-Quartett diese Problematik. Es verdeutlicht, wie vier Datensätze trotz identischem Mittelwert und identischer Varianz graphisch total verschieden aussehen können. Die zusammenfassenden Statistiken der vier Datensätze von Anscombe sind folgendermassen:
- Der Mittelwert von x hat bei allen vier Datensätzen den Wert 9
- Der Mittelwert von y hat bei allen vier Datensätzen den Wert 7.5
- Die Varianz von x hat bei allen vier Datensätzen den Wert 11
- Die Varianz von y hat bei allen vier Datensätzen den Wert 4.12
- Die Korrelation zwischen x und y ist in allen vier Datensätzen 0.816
- Die Gleichung für eine lineare Regression ist bei allen Datensätzen y = 0.5x + 3
Schaut man sich diese Werte an, lässt sich intuitiv schlussfolgern, dass diese Datensätze einander sehr ähnlich, wenn nicht identisch sind. Folglich könnte man auch denken, dass sie visuell grosse Ähnlichkeit aufweisen. Stellt man sie erstmal graphisch dar, wird schnell klar, dass die Ähnlichkeit doch nicht so gross wie erahnt ist.
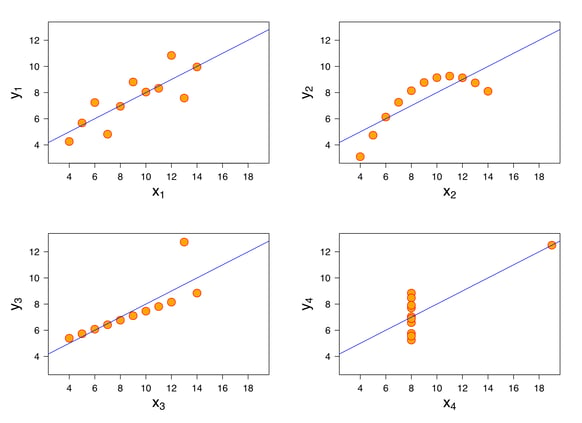
Erst mit der Visualisierung werden die Beziehungen zwischen den einzelnen Datenpunkten klarer. Während der erste Datensatz vermutlich einen linearen Zusammenhang mit etwas Varianz aufweist, scheint Datensatz drei einen fast perfekten linearen Zusammenhang mit nur minimal abweichenden Residuen aufzuweisen. Lediglich ein Ausreisser steht wirklich im «Schilf». Beim letzten Datensatz sieht es aus, als wäre kein Zusammenhang zwischen x und y. Doch auch hier kann wieder ein Ausreisser beobachtet werden. Datensatz Nummer zwei weist definitiv einen Zusammenhang auf, wobei dieser nicht wirklich linear ist.
Ein noch extremeres Beispiel dafür ist das «Datasaurus Dozen», wobei auch hier wieder alle Datensätze den gleichen Mittelwert sowie die gleiche Varianz und den gleichen Korrelationskoeffizienten aufweisen.
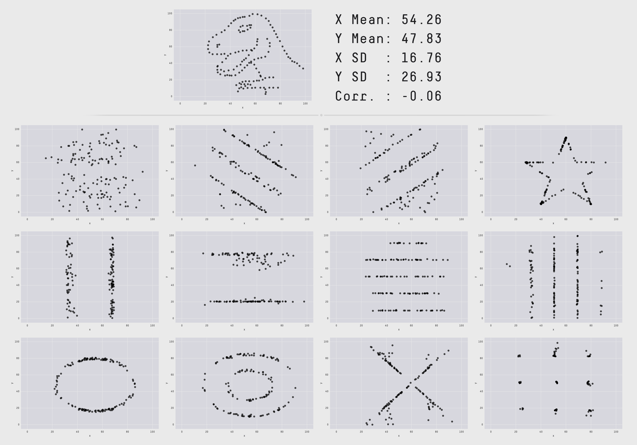
Eine intuitive Schlussfolgerung wäre auch hier, dass es sich um sehr ähnlich bis identische Zusammenhänge handeln muss. Doch wie erkennbar ist, nehmen einige Datensätze bei der graphischen Darstellung die Form eines Dinosauriers oder eines Sterns an.
Als Fazit kann festgehalten werden, dass es wichtig ist, Datensätze zu visualisieren und nicht bloss die zusammenfassenden deskriptive Statistik zu analysieren. Denn der Schein mag ganz offensichtlich trügen und potenziell in diesem Kontext schlechte Entscheidungen zur Folge haben.
