“Statistics are like bikinis. What they show is stimulating, but what they hide is the main thing” – Aaron Levenstein.
In view of the enormous amounts of data, it is impossible to imagine life without statistics these days. Statistical calculations are used in practically every imaginable area. On the one hand, they are used to calculate important key figures in various economic topics such as gross domestic product (GDP) or inflation. On the other hand, statistics also play an equally important role in the private sector. From sector to sector there are different applications where it could be used. For example, in retail trade and online trade, the average value of the customer’s shopping basket can be measured. This key figure can then be used to measure whether promotions or a different placement of articles have a positive effect on the value of the shopping basket and thus lead to more sales.
In call centers, the average time taken to process a telephone call can be calculated. If a certain employee takes significantly longer to make a telephone call than the average, this can be an indicator that the employee requires additional training. Departmental training can even have the effect of reducing the overall average processing time.
Statistics can also be relevant for describing your own offerings. For example, the service level or service grade are widely used key figures for the service level offered. In the case of OCR software, the service level is often described by extraction rates and sensitivity, which are also determined by statistical calculations.
However, as the quote from Aaron Levenstein makes clear, statistics can look nice and provide some clues, but the background and calculations are the most important part of any statistic. Graphical representation as well as certain key figures such as location or dispersion parameters should not be considered in isolation. As Francis Anscombe noted in 1973, different data sets can have the same variance and mean value, but they can look completely different graphically. But before we go into this further, I will first briefly describe the most important terms.
What are mean value, standard deviation and variance?
The mean value of a data set is simply the average of these data. For example, the mean has a value of 10 for a data set containing the numbers 5, 10, and 15.
The standard deviation is a measure of the dispersion of the values around the mean. For a data set with a large number of values, the standard deviation shows how far these data are distributed between the minimum and the maximum and how closely they cluster around the mean value. This distribution of the data points can be shown in a function curve. Depending on the nature of the data, this curve has a different form. If we have a normal distribution, it resembles a bell shape. For example, for the height of footballers, the mean value could be 1.80m and the standard deviation (σ) 0.1m. Rather few footballers are over 2.00m or under 1.60m, but more are between 1.70m and 1.90m. Most of the footballers will be within a standard deviation below or above the mean of 1.80m. Assuming a normal distribution ~ 68% of the footballers would be between 1.70m and 1.90m. ~ 95% of all footballers would be within two standard deviations. In this case ~ 95% would be between 1.60m and 2.00m. The remaining ~ 5% of the footballers would be over 2.00m or under 1.60m.
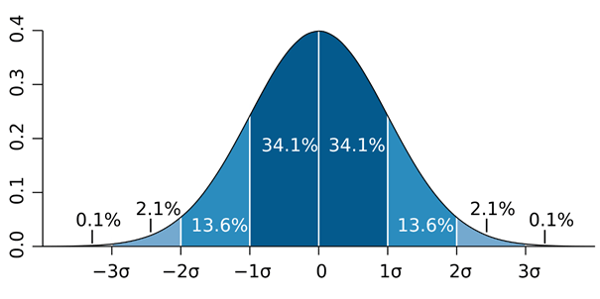
So while the standard deviation shows how the values are distributed around the mean value, the variance is merely the square of the standard deviation and is thus also a measure of dispersion that describes the distribution of observed values around the expected value. However, squaring also squares the unit, so in our example the unit would no longer be meters (m) but square meters (m2), which is not a very meaningful measure in relation to body size.
Summary statistics do not tell the whole story
These three described parameters make it possible to describe a large, complex data set with only a few key figures relatively well. However, there is a danger of relying only on these summary statistics and ignoring the overall distribution. The calculation of these parameters is therefore useful, but should only be part of the actual data analysis. In the following I will explain why this is so.
As indicated earlier, the Anscombe Quartet demonstrates this problem. It illustrates how four data sets can look totally different graphically despite identical mean and variance. The summary statistics of Anscombe’s four data sets are as follows:
- The mean value of x has the value 9 for all four data sets
- The mean value of y has the value 7.5 for all four data sets
- The variance of x has the value 11 in all four data sets
- The variance of y has the value 4.12 for all four data sets
- The correlation between x and y in all four data sets is 0.816
- The equation for a linear regression is y = 0.5x + 3
Looking at these values, one can intuitively conclude that these records are very similar, if not identical. Consequently, one could also think that they are visually very similar. If you look at them graphically, it quickly becomes clear that the similarity is not as great as you might have thought.
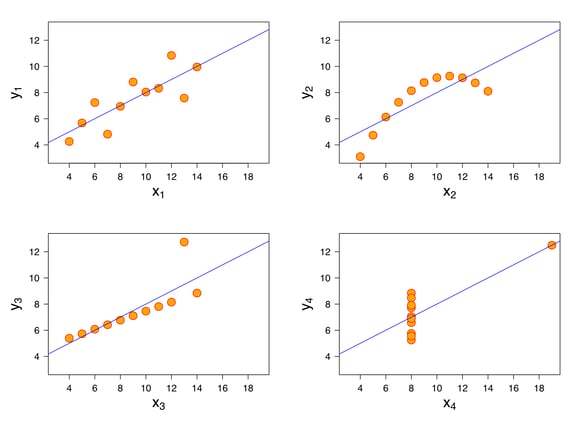
Only with visualization do the relationships between the individual data points become clearer. While the first dataset probably shows a linear relationship with some variance, dataset three seems to show an almost perfect linear relationship with only minimal residuals. Only one outlier is really in the «reed». In the last data set, it looks as if there is no correlation between x and y. But again, an outlier can be observed. Data set number two definitely shows a connectedness, but it is not really linear.
An even more extreme example is the «Datasaurus Dozen», where again all data sets have the same mean value, variance and correlation coefficient.
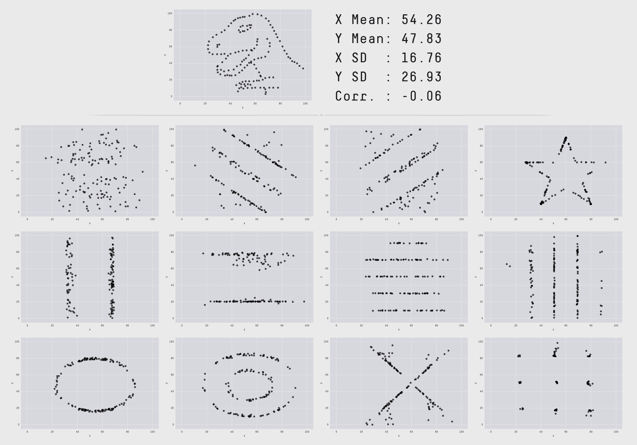
An intuitive conclusion would also be here that the connections must be very similar if not identical. However, as can be seen, some data sets even take the form of a dinosaur or a star in the graphical representation.
In conclusion, it is important to visualize data sets and not just to analyze the summary descriptive statistics. After all, appearances are obviously deceptive and may potentially lead to bad decisions in this context.
